在信號處理領域，頻域分析是至關重要的，但很多人在編程實現這一過程中遇到了困難。這恰恰是我們今天需要重點探討的核心議題。

直接FFT的結果與調整

在執行FFT分析后，結果呈現出了明顯的規律。例如，信號的起始部分對應的是頻率區間[0,fs/2]，而結束部分則對應[-fs/2,0]。在實際操作中，必須將零頻點放置在頻譜的中央，這非得借助fftshift函數不可。以一個具體項目為例，在分析一段采集到的音頻信號時，未經fftshift處理的FFT結果讓人難以直接識別頻率分布。但經過調整，頻譜圖便清晰地展現了正負頻率的分布。這一步驟對于聲音信號的頻域分析等類似工作極為關鍵。

我們得知，處理FFT結果需要采用截取正頻段的方法。這主要有兩種方式：一是在fftshift后取后半部分，二是直接在fft結果中取前半部分。這兩種方法得出的結果并無差異。就好比分析心電圖信號，不管選用哪種截取方式，都是為了提取正頻段成分，以便進行與疾病相關的頻率特征分析。

t_s = 0.01; %采樣周期
t_start = 0.5; %起始時間
t_end = 5;     %結束時間
t = t_start : t_s : t_end;
y = 1.5*sin(2*pi*5*t)+3*sin(2*pi*20*t)+randn(1,length(t));  %生成信號

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%頻譜%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
y_f = fft(y); %傅里葉變換
subplot(5,1,1);
plot(t,y);title('original signal');   %繪制原始信號圖
Druation = t_end -t_start;  %計算采樣時間
Sampling_points = Druation/t_s +1;  %采樣點數，fft后的點數就是這個數
f_s = 1/t_s; %采樣頻率
f_x = 0:f_s/(Sampling_points -1):f_s;  %注意這里和橫坐標頻率對應上了，頻率分辨率就是f_s/(Sampling_points -1)
t2 = f_x-f_s/2;
shift_f = abs(fftshift(y_f));
subplot(5,1,2);
plot(f_x,abs(y_f));title('fft transform');
subplot(5,1,3);
plot(f_x-f_s/2,shift_f);title('shift fft transform');  %將0頻率分量移到坐標中心
subplot(5,1,4);
plot(t2(length(t2)/2:length(t2)),shift_f(length(shift_f)/2:length(shift_f)));title('shift fft transform');   %保留正頻率部分
subplot(5,1,5);
plot(f_x(1:length(f_x)/2),abs(y_f(1:length(f_x)/2)));title('fft cut');  %直接截取fft結果的前半部分

奈奎斯特定理的作用

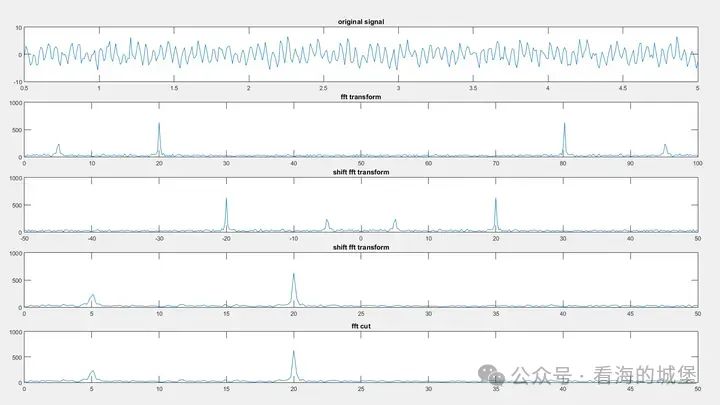
奈奎斯特定理在頻域分析中扮演著核心角色。它指出，信號的采樣速度必須高于其最高頻率的兩倍。比如，對于雷達信號，如果雷達發射的最高頻率是10MHz，那么采樣速度至少要是20MHz。如果低于這個標準，就會導致頻譜重疊。實驗表明，如果采樣速度不夠，采集到的頻譜圖中會出現錯誤頻率，這會影響到所有頻域處理結果的精確度。

換個角度審視，此定理明確了頻域分析中基礎采樣準則的設定。比如，在處理地震波信號時，若不依照奈奎斯特定理，低頻地震信號可能會與高頻噪聲混淆，進而造成地層結構關鍵信息的識別困難。

功率譜的求法

計算功率譜有倆種方法。一種是用傅立葉變換的平方除以區間長度來算，這方法挺簡單，容易理解。在MATLAB編程里，我們根據這個公式就能得到結果。例如，針對描述粒子運動軌跡的離散信號，用這個方法算功率譜，就能看出粒子在不同頻率上的能量分布情況。

還有一法是采用自相關函數執行傅里葉轉換。從理論層面分析，這兩種手段的成果本應相同。但實際操作中，例如在分析含噪電子設備輸出信號時，我們發現自相關函數法在降噪效果上更為突出，繪制的曲線也更加平滑。這好比在喧鬧場合努力辨識對方說話，運用自相關函數傅里葉轉換這一技術，能更高效地去除噪音干擾，進而更清晰地呈現出信號的功率譜特征。

Fs = 1000;
nfft = 1000;  %fft采樣點數

%產生序列
n = 0:1/Fs:1;
xn = cos(2*pi*100*n) + 3*cos(2*pi*200*n)+(randn(size(n)));
subplot(5,1,1);plot(xn);title('加噪信號');xlim([0 1000]);grid on
%FFT
Y = fft(xn,nfft);
Y = abs(Y);
subplot(5,1,2);plot((10*log10(Y(1:nfft/2))));title('FFT');xlim([0 500]);grid on
%FFT直接平方
Y2 = Y.^2/(nfft);
subplot(5,1,3);plot(10*log10(Y2(1:nfft/2)));title('直接法');xlim([0 500]);grid on
%周期圖法
window = boxcar(length(xn));  %矩形窗
[psd1,f] = periodogram(xn,window,nfft,Fs);
psd1 = psd1 / max(psd1);
subplot(5,1,4);plot(f,10*log10(psd1));title('周期圖法');ylim([-60 10]);grid on
%自相關結果
cxn = xcorr(xn,'unbiased');  %計算自相關函數
%自相關法
CXk = fft(cxn,nfft);
psd2 = abs(CXk);
index = 0:round(nfft/2-1);
k = index*Fs/nfft;
psd2 = psd2/max(psd2);
psd2 = 10*log10(psd2(index+1));
subplot(5,1,5);plot(k,psd2);title('間接法');grid on

直接法與周期圖法對比

編寫代碼時，我們運用直接法，通過傅立葉變換的平方除以區間長度來求得功率譜。這一方法與MATLAB中的periodogram函數所得結果相同。在分析機械振動信號時，我們對比了這兩種計算功率譜的方法。結果顯示，在數據量不多且信號頻率成分簡單的情況下，兩種方法得出的結果非常接近。這一發現為我們在編寫頻域分析代碼時提供了更多選擇，使我們能根據實際情況挑選出更易理解或計算速度更快的方案。

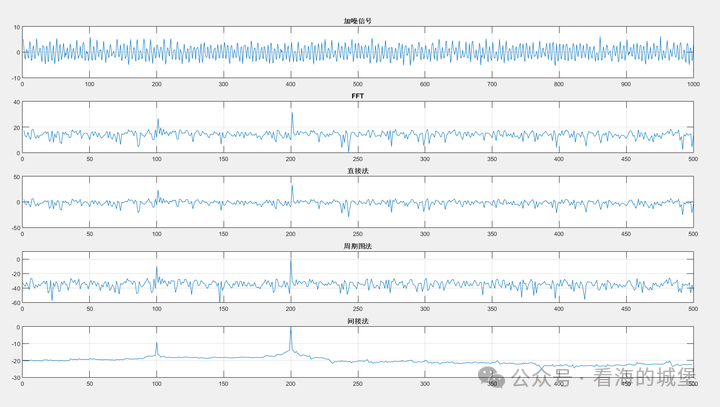
工業監測系統若要依賴實時功率譜來預測故障，這一點極為關鍵。以風力發電機的振動監控為例，我們需根據硬件條件和信號特點，巧妙選擇計算功率譜的方法。最重要的是，要能快速且精確地識別出潛在的危險頻率信號。

倒頻譜的計算與含義

實倒頻譜函數用于計算倒頻譜，MATLAB手冊中指出其計算步驟是先將信號轉換為頻譜，接著轉為對數形式，最后執行傅立葉逆變換。但倒頻譜的定義是將信號轉成功率譜，隨后進行對數處理，再進行傅立葉逆變換。兩者間的差異可能源于功率譜是頻譜值的平方，對數處理后，平方變成了系數2，但這對于后續計算影響微乎其微，所以近似結果并無差異。

在仿真實驗里，我們需要留意倒頻譜的作用，需要親手制作一組調頻信號。舉例來說，對那些高頻（如50Hz、100Hz、200Hz）和低頻（如5Hz、10Hz、20Hz）的信號進行調整，接著分別畫出低頻、高頻和調頻信號的時域圖和頻譜圖。這種調頻信號的處理方法，在通信信號分析領域應用很廣，有助于提高信號傳輸的效率和穩定性。

倒頻譜在信號處理中的體現

sf = 1000;
nfft = 1000;
x = 0:1/sf:5;
y1=10*cos(2*pi*5*x)+7*cos(2*pi*10*x)+5*cos(2*pi*20*x)+0.5*randn(size(x));
y2=20*cos(2*pi*50*x)+15*cos(2*pi*100*x)+25*cos(2*pi*200*x)+0.5*randn(size(x));
for i = 1:length(x)
    y(i) = y1(i)*y2(i);
end
subplot(3,3,1)
plot(y1);xlim([0 5000]);title('y1');
subplot(3,3,2)
plot(y2);xlim([0 5000]);title('y2');
subplot(3,3,3)
plot(y);xlim([0 5000]);title('y=y1*y2');

t = 0:1/sf:(nfft-1)/sf;
nn = 1:nfft;
subplot(3,3,4)
ft = fft(y1,nfft);
Y = abs(ft);
plot(0:nfft/2-1,((Y(1:nfft/2))));
title('fft_y_1');
ylabel('幅值');xlim([0 300]);
grid on;
subplot(3,3,5)
ft = fft(y2,nfft);
Y = abs(ft);
plot(0:nfft/2-1,((Y(1:nfft/2))));
title('fft_y_2');
ylabel('幅值');xlim([0 300]);
grid on;
subplot(3,3,6)
ft = fft(y,nfft);
Y = abs(ft);
plot(0:nfft/2-1,((Y(1:nfft/2))));
title('fft_y');
ylabel('幅值');xlim([0 300]);
grid on;

subplot(3,3,7)
z = rceps(y);
plot(t(nn),abs(z(nn)));
title('z=rceps(y)');ylim([0 0.3]);
xlabel('時間(s)');
ylabel('幅值');
grid on;
subplot(3,3,8)
yy = real(ifft(log(abs(fft(y))))); %信號→傅里葉→對數→傅里葉逆變換
plot(t(nn),abs(yy(nn)));
title('real(ifft(log(abs(fft(y)))))');ylim([0 0.3]);
xlabel('時間(s)');
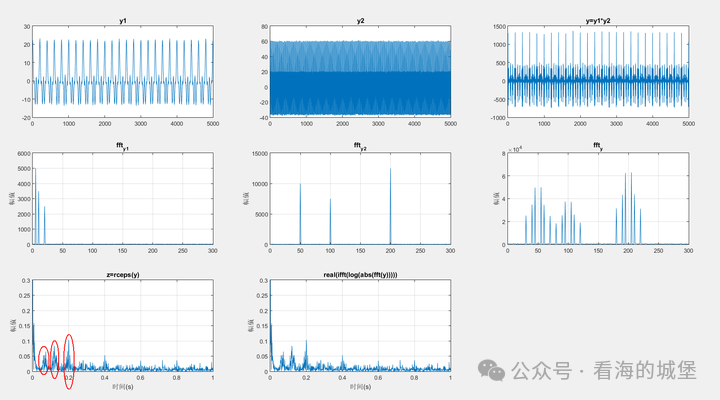
ylabel('幅值');
grid on;

以特定調制信號為例，例如某些信號中帶有20Hz、10Hz和5Hz等低頻部分。在常規的FFT_y分析中，這些低頻部分以邊緣頻帶的形式出現，難以準確判斷其頻率。但在倒頻譜分析中，這些部分卻很容易被識別。這好比在黑夜中，一雙隱藏的眼睛在FFT_y分析中難以發現，而在倒頻譜分析中卻能立刻被“照亮”，顯示出其特征。在無線電通信的信號分析中，倒頻譜分析這種處理類似問題的能力對工程師來說非常寶貴，它能夠幫助他們快速發現并解讀微弱的低頻信號。

關于項目操作中選用頻域分析方法的問題，我想聽聽大家的意見：面對不同項目的具體特點，你們是如何做出選擇的？歡迎在評論區留下你們的想法。若這篇文章對您有所啟發，不妨點贊或分享給更多人。